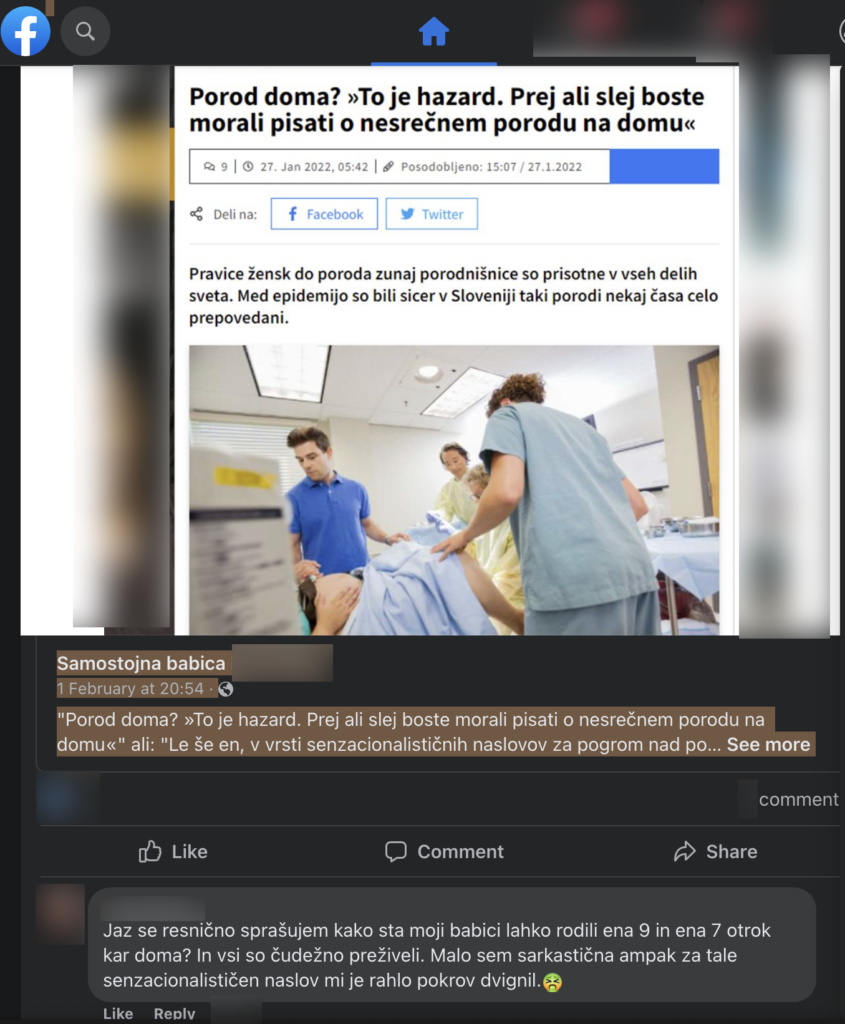
Ok. This post will mostly not be about safety of home delivery, versus hospital delivery. Really quick and dirty google search will answer this for you. Very briefly, in the U.S. on average about 14 out 10.000 home deliveries results in death, while about 3 out of 10.000 hospital deliveries result in deaths according to Reuters.For those mathematically challenged, this means that it is four times more likely that your newborn will die in the U.S. if you deliver at home. This does not really hold in Europe, as they screen for eligibility before they allow home births. Therefore, completely free choice in the EU was always a myth – if you are considered to be at risk, you cannot give birth at home in the EU, the article above claims.
I wanted to write about something else, though. This comment is (a) a nice demonstration of Dunning-Krueger and (b) a nice demonstration of stats ignorance. We have discussed Dunning – Krueger before, so no need to flog this dead horse. But the stats issue…
I wonder what the family dinners looked like at the comment poster’s (; OP) home. How often did the two grandmas discuss how many of their children died in childbirth or immediately after? Was this a topic before or after dessert? Was there ever a time, when one grandma said:
“How nice to have you all here at this Sunday dinner. Well I say all, but I mean those of you who survived. Perhaps you are not aware, but you had additional X brothers and sisters who all died. The first one asphyxiated, this was in XXX, the second one… Why are you all so glum? Apple pie, anyone?”
In personal experience, it is hard to talk about dead siblings with offspring. Therefore it is likely that the OP has no actual idea, what the birth success rate was in their family, and claiming that of all those who survived, a 100% survival rate was observed, is perhaps not such a devastatingly effective argument as the poster imagines.
Secondly, the actual stats are clear, and trying to change them by providing an anecdotal sample of two is doomed to fail. Even if both of OP grandmothers suffered no miscarriages or stillbirths ever (which we cannot be certain of), the sample (N=2) is far too small to provide any real significance or to invalidate actual research.
I fondly recall my Thesis supervisor Stephen, saying that in every family or peer group, there is always someone who argues against wearing seatbelts in cars because they have an acquaintance of an acquaintance who knows someone who drove into a lake, and would have drowned if they were wearing a seatbelt. His response to that would be that:
“Your sample of one, even if it exists, is an outlier and does not in any way prove that wearing seatbelts is optional. Wearing seatbelts has saved many more lives, than endangered them.”
An outlier is a response that differs from the trend so wildly, that we need to delete it from the data set in order to get any sort of valid results. Outlier removal, when certain statistical assumptions are met, is a common practice. Here is an article (with pictures) on why, how and when do we do it. And Another. Claiming that because you know someone who does not follow the trend, the whole trend is invalid beautifully demonstrates ignorance of what statistics actually tells you – in its commonest form, it tells you the probability of a certain percentage of the population doing something. That is, something like:
“Out of one hundred cases of people getting a booster shot, 33 to 37 (or whatever the current stats are) will still get COVID, but out of those 33 – 37 people, less than one will suffer total body collapse. “
Statistics will practically never tell you the likelihood of one specific individual doing something. So nothing like:
“If you personally get covid, vaccines will protect you every time.”
And, conversely statistics will never tell you
“Vaccines don’t work.”
The first false example above is about an individual, which statistics are somewhat bad at evaluating, and too absolute. I mean a scientist might tell you that it is very likely that a vaccine will protect you (and not mention that very likely to them means, say 77% of the cases, because people are very bad at understanding statistics), but they are very unlikely to claim absolutes (see what I did there? very unlikely here meaning, IMO, 99.9%), because their claims come from trends in the population, not individuals, and they only talk about what data shows for every hundred cases, not for David Modic, specifically.
The second false example is again too absolute, but also statistically unprovable. I mean, Ivermectin works, that is a fact. It just works for horses when they have worms, not people with COVID. So, no scientist ever said it is ineffective, they just said it is ineffective against COVID. In the same vein, it is not possible to prove that Vaccines do not work. First of all, there is a growing empirical body of evidence rubbishing this claim, but also even if there weren’t, it is exceedingly hard proving a negative. An individual might claim that Anti-COVID vaccines are ineffective agains COVID, but that would be, empirically, easy to disprove. Even that would not say anything about the vaccine being ineffective against double vision or tinnitus. I mean it probably is ineffective, as both are symptoms and neither is solely caused by a virus, but, proving that something isn’t x, does not prove that therefore it is everything that is x. That is a mouthful. Simply put, proving that ice cream does not melt at absolute zero (-273C), does not prove that it melts at all other temperatures (like, say -200C). Issuing blanket statements is just bogus. Or proving that beating children does not insure school success, does not prove that they will become brilliant academics, if you keep everything else the same, but stop beating them.
Another thing which I already expanded upon is that the initial post hints at why some people will oppose COVID vaccination, based on false or anecdotal claims. It is enough that someone somewhere states that vaccines do not work, or that “everybody knows that x“, in order to make individuals feel they have a counterargument that invalidates research that has taken hundreds or thousands of hours of combined effort of professional researchers.
It is quite hard not to get angry at that level of ignorance and self-absorption. How likely is it that someone who has chipped away at something for decades and has been vigorously tested and challenged by colleagues every step of the way, has missed something that two minutes of YouTube reveals? Seriously, how likely is it? And how full of yourself do you have to be to even get into a headspace where you assume that ten minutes of effort will push you to the forefront of science and let you teach all those fools who spent years perfecting their skills and craft, what is what.
So, thank you for the comment, OP and thank you for providing teaching materials to all of us.
